MLE of the psychometric function: theory
In the simpler case of MLE, we have some iid (independent and identically distributed) observations and we want to estimate from the parametric family of distributions, which is the most likely distribution. In psychophysics often we have some observations \(k_1, k_2,..k_n\) that are independent but no identically distributed because they are indexed by another variable \(x_1,x_2,...,x_n\). For example, \(k_1\) could be the number of trials (from a total of 100 trials) for which the observer reports that can see a dim stimulus when the luminance of the stimulus is \(x_1\); \(k_2\) the number of trials in which the observer reports that can see the stimulus for luminance \(x_2\) and so on. We need to use a generalization of the likelihood function that includes the index \[L(\theta|x,k)=f(x,k|\theta)\]
Suppose that we have the following independent observations
library(ggplot2)
k <- c(10, 26, 73, 94, 99) #our observations, number of trials in which the observer reports that can see the stimulus (from a total of 100 trials)
x <- c(.2, .4, .6, .8, 1) # the observations are indenxed by x, intensity
n <- 100 # total number of trialsWhen we fitted MLE for some distributions (for example for the estimation of the parameters of the binomial distribution), we plotted the observations in a x-axis and then used the y-axis to plot the value of the probability density function. Now, we cannot used this kind of plot because the observations k are indexed by x so that every \(k_i\) comes from a different distribution. Let’s plot the observations as a function of the indexed variable instead
dat<-data.frame(x,k) #we plotted our observations in the x-axis
p<-ggplot(data=dat,aes(x=x,y=k))+geom_point(size=4)
p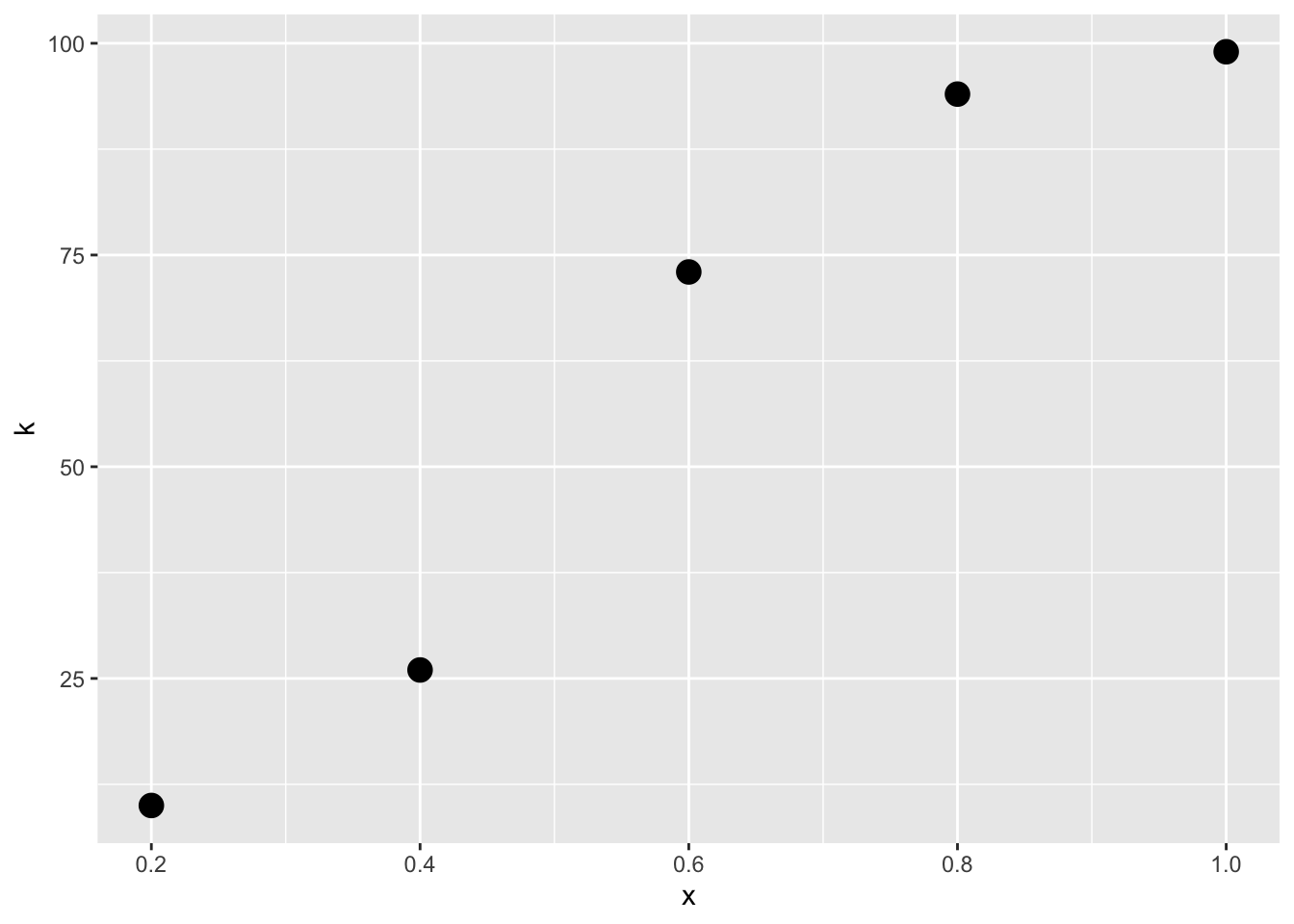 We don’t know the exact probability density functions for \(k_1, k_2,..k_n\) , but we know that the shape is the shape of the binomial distribution where n is 100 and p is indexed by x according to cumulative normal distribution with parameters \(\mu\) and \(sigma\) \[p=\Phi(x,\mu,\sigma).\] Then, the probability density function for \(k_i\) is \[f(x_i,k_i\mid\theta)=f(x_i,k_i\mid n,p)=f(k_i\mid n,\Phi(x_i,\mu,\sigma))=\binom{n}{k_i}\Phi(x_i,\mu,\sigma)^{k_i}(1-\Phi(x_i,\mu,\sigma))^{n-{k_i}}\] where n=100.
We don’t know the exact probability density functions for \(k_1, k_2,..k_n\) , but we know that the shape is the shape of the binomial distribution where n is 100 and p is indexed by x according to cumulative normal distribution with parameters \(\mu\) and \(sigma\) \[p=\Phi(x,\mu,\sigma).\] Then, the probability density function for \(k_i\) is \[f(x_i,k_i\mid\theta)=f(x_i,k_i\mid n,p)=f(k_i\mid n,\Phi(x_i,\mu,\sigma))=\binom{n}{k_i}\Phi(x_i,\mu,\sigma)^{k_i}(1-\Phi(x_i,\mu,\sigma))^{n-{k_i}}\] where n=100.
Given that \(k_i\) are independent, the join density function is the multiplication of the probability density function for each \(k_i\) \[f(k\mid \theta)=f(k_1,k_2...k_n\mid \mu,\sigma)=f(x_1,k_1\mid \mu,\sigma)f(x_2,k_2\mid \mu,\sigma)...f(x_n,k_n\mid \mu,\sigma)=\] \[=\binom{n}{k_1}\Phi(x_1,\mu,\sigma)^{k_1}(1-\Phi(x_1,\mu,\sigma))^{n-{k_1}}...\binom{n}{k_n}\Phi(x_n,\mu,\sigma)^{k_n}(1-\Phi(x_n,\mu,\sigma))^{n-{k_n}}\] that when considered as a function of the parameters is the likelihood function \[L(\theta\mid k)=L(\mu,\sigma\mid k)=\] \[=f(k\mid \theta)=\binom{100}{10}\Phi(.2,\mu,\sigma)^{10}(1-\Phi(.2,\mu,\sigma))^{100-10}...\binom{100}{99}\Phi(1,\mu,\sigma)^{99}(1-\Phi(1,\mu,\sigma))^{100-99}\] and \[log(L)=\sum_{i=1}^{n} \left \{ log\binom{n}{k_i}+k_i log(\Phi(x_i,\mu,\sigma))+(n-k_i) log(1-\Phi(x_i,\mu,\sigma)) \right \}\]
Given that the first log does not depend on the parameters \(\mu\) and \(\sigma\) usually is dropped
logL<-function(p) { # strictly is not log(L) because of the dropped term
phi<-pnorm(x,p[1],p[2]) #mu: p[1], sigma:p[2]
sum( k*log(phi)+(n-k)*log(1-phi) )
}Let’s calculate \(log(L)\) for two pairs of parameters
logL(c(.6,.15))## [1] -223.9472logL(c(.3,.4))## [1] -226.2905logL(c(.6,.15))>logL(c(.3,.4))## [1] TRUE\(\mu=.6\) and \(\sigma=.15\) describe the observations k better. Let’s plot the predicted observations using these two pairs of parameters
xSeq<-seq(0,1,.01)
kPred1<-n*pnorm(xSeq,.6,.15) # the expected value of a binomial distribution with parameters n and p is n*p
kPred2<-n*pnorm(xSeq,.3,.4)
curve1<-data.frame(xSeq,kPred1)
curve2<-data.frame(xSeq,kPred2)
p+geom_line(data=curve1,aes(x=xSeq,y=kPred1,color='p=c(.6,.15)'))+
geom_line(data=curve2,aes(x=xSeq,y=kPred2,color='p=c(.3,.4)'))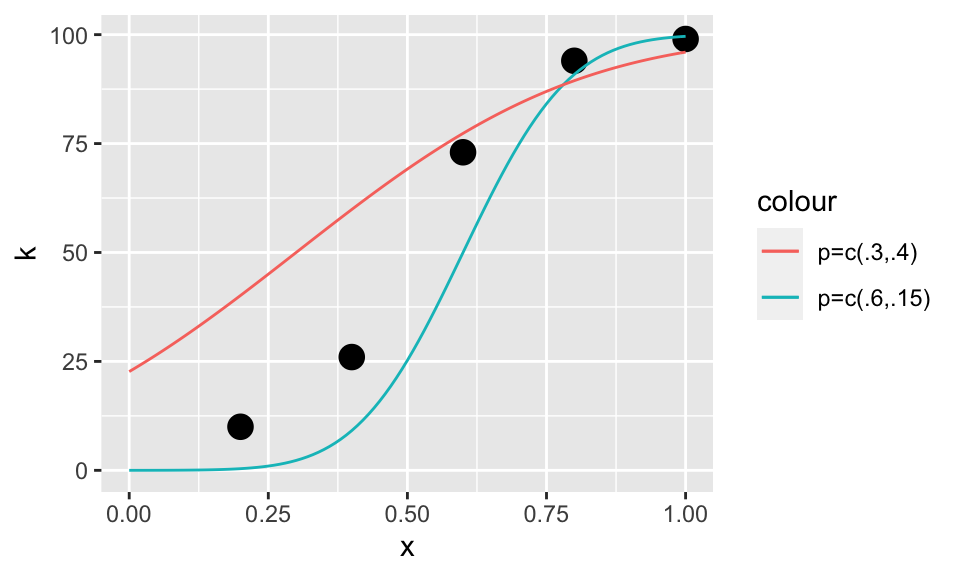 Indeed, it seems that \(\mu=.6\) and \(\sigma=.15\) describe the observations k better. Let’s maximize it properly
Indeed, it seems that \(\mu=.6\) and \(\sigma=.15\) describe the observations k better. Let’s maximize it properly
negLogL<-function(x) -logL(x)
estPar<-optim(c(.7,.7), negLogL)## Warning in pnorm(x, p[1], p[2]): NaNs producedMLEparameters<-estPar$p
MLEparameters## [1] 0.4933163 0.2043634kMLE<-n*pnorm(xSeq,MLEparameters[1],MLEparameters[2])
curveMLE<-data.frame(xSeq,kMLE)
p+geom_line(data=curveMLE,aes(x=xSeq,y=kMLE))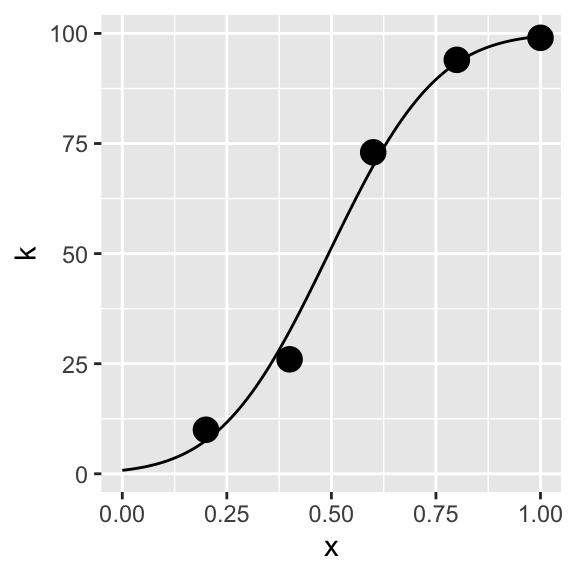
References
Knoblauch, K., & Maloney, L. T. (2012). Modeling Psychophysical Data in R. New York: Springer.
Prins, N., & Kingdom, F. A. A. (2010). Psychophysics: a practical introduction. London: Academic Press.