MLE of the psychometric function: practice
Fitting (minimizing directly the negative log-likehood)
Let’s suppose that we present a stimulus at different luminances and we ask the observer whether can or cannot see the stimulus. We use 5 luminance levels and for each level we present the stimulus 100 times. Here some hypothetical data
library('ggplot2')
n <- 100
x <- c(.2, .4, .6, .8, 1) # luminance
k <- c(10, 26, 73, 94, 97) # number of times that the observer reports that can see the stimulus
y <- k/n # proportion
dat <- data.frame(x, y, k, n)
p <- ggplot()+
geom_point(data=dat,aes(x=x,y=y))
p
Let’s fit a cumulative normal distribution whose parameters are estimated using MLE
nll <- function(p) { # negative log likelihood
phi <- pnorm(dat$x, p[1], p[2])
-sum(dat$k * log(phi) + (dat$n - dat$k) * log(1 - phi) )
}
para <- optim(c(.7, .7), nll)$par## Warning in pnorm(dat$x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145There is a warning because during the optimization process sometimes phi is equal to 0 or 1 and then \(log(phi)\) or \(log(1-phi)\) is -Inf, but this does not affect the fitting procedure as we are searching for the minimum of \(nll\).
xseq <- seq(0, 1, .01)
yseq <- pnorm(xseq, para[1], para[2])
curve <- data.frame(xseq, yseq)
p + geom_line(data = curve,aes(x = xseq, y = yseq))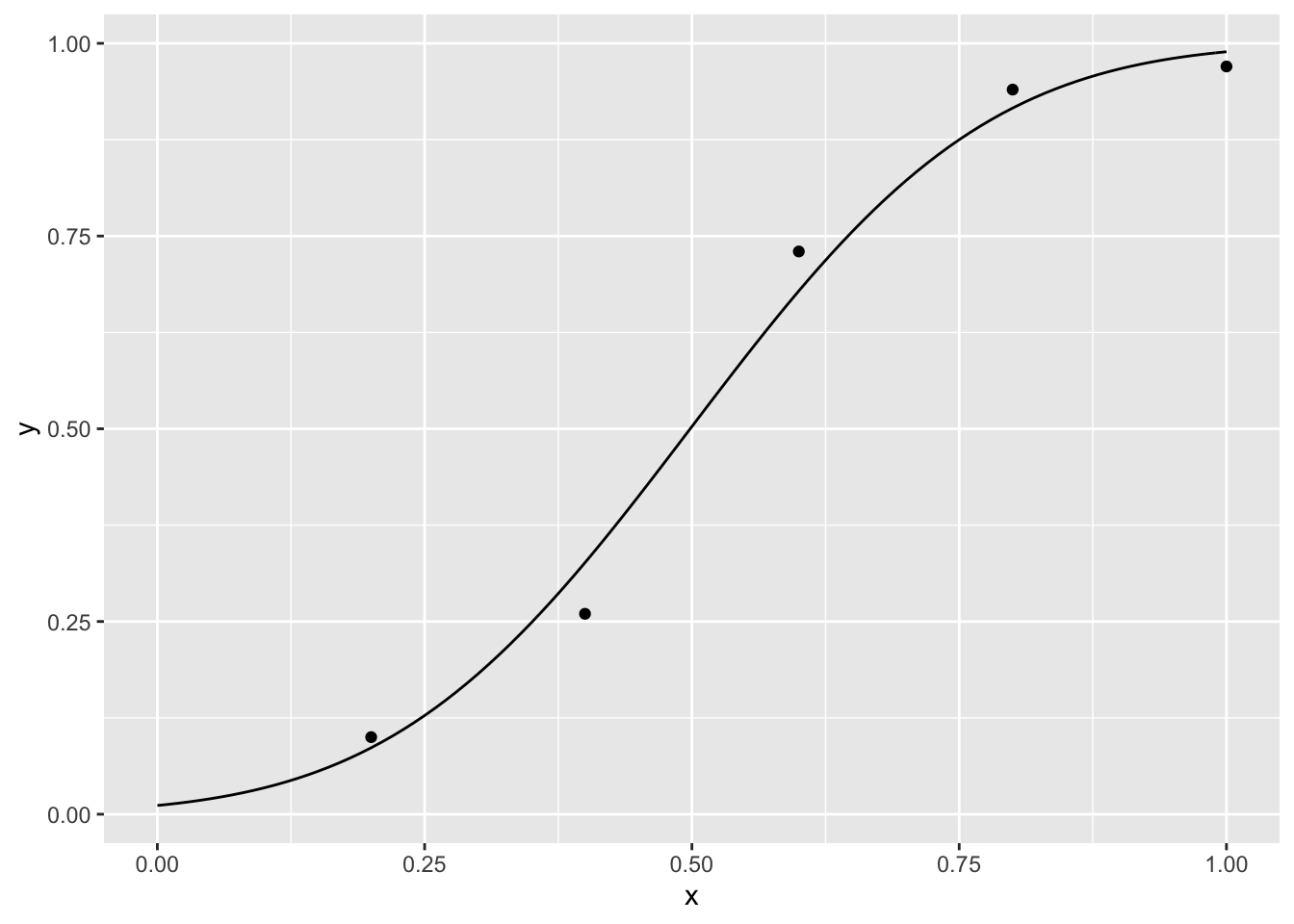
Better coding
In the previous example the function nll that is passed to the functional optim picks up the data that is in the global environment. It is a better practice to pass into the function the data as an argument
nll <- function(p, d) {
phi <- pnorm(d$x, p[1], p[2])
-sum(d$k * log(phi) + (d$n - d$k) * log(1 - phi) )
}
para <- optim(c(.7, .7), nll, d = dat)$par # we need to pass the data to nll## Warning in pnorm(d$x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145MLE is indeed well suited for the use of closures (functions that create functions). We can create a function that creates from the data a negative log-likelihood function that depends only on the parameters.
create_nll <- function(d){ #creates a function of the parameters from the data
function(p) {
phi <- pnorm(d$x, p[1], p[2])
-sum(d$k * log(phi) + (d$n - d$k) * log(1 - phi) )
}
}
nll <- create_nll(dat)
para <- optim(c(.7, .7), nll)$p # we don't need to pass the data to nll## Warning in pnorm(d$x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145We can also pass the function to fit
create_nll <- function(d, fun){
function(p) {
phi <- fun(d$x, p)
-sum(d$k * log(phi) + (d$n - d$k) * log(1 - phi) )
}
}
cum_normal_fun <- function(x,p) pnorm(x, p[1], p[2])
nll <- create_nll(dat, cum_normal_fun)
para <- optim(c(.7, .7), nll)$p # we don't need to pass the data to nll## Warning in pnorm(x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145and the names of the variables
create_nll <- function(d, fun, X, nyes, N){
function(p) {
phi <- fun(d[[X]], p)
-sum(d[[nyes]] * log(phi) + (d[[N]] - d[[nyes]]) * log(1 - phi) )
}
}
cum_normal_fun <- function(x,p) pnorm(x, p[1], p[2])
nll <- create_nll(dat, cum_normal_fun, 'x', 'k', 'n')
para <- optim(c(.7, .7), nll)$p # we don't need to pass the data to nll## Warning in pnorm(x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145If we want to pass the name of the variables without quotes, we can do
create_nll <- function(d, fun, X, nyes, N){
X <- deparse(substitute(X))
nyes <- deparse(substitute(nyes))
N <- deparse(substitute(N))
function(p) {
phi <- fun(d[[X]], p)
-sum(d[[nyes]] * log(phi) + (d[[N]] - d[[nyes]]) * log(1 - phi) )
}
}
cum_normal_fun <- function(x,p) pnorm(x, p[1], p[2])
nll <- create_nll(dat, cum_normal_fun, x, k, n)
para <- optim(c(.7, .7), nll)$p ## Warning in pnorm(x, p[1], p[2]): NaNs producedpara## [1] 0.4984123 0.2187145m-alternatives forced choiced
Let’s suppose that in each trial we present one stimulus to the left or right of the fixation point and the observer needs to decide in which location the stimulus was presented. We use five luminance levels and for each level we present the stimulus 100 times. Here some hypothetical data
library('ggplot2')
n <- 100
x <- c(.2, .4, .6, .8, 1) #luminance
k <- c(59, 56, 69, 84, 96) # number of times that the observer reports that can see the stimulus
y <- k/n
dat <- data.frame(x, k, y)
p<-ggplot()+
geom_point(data=dat,aes(x=x,y=y))
p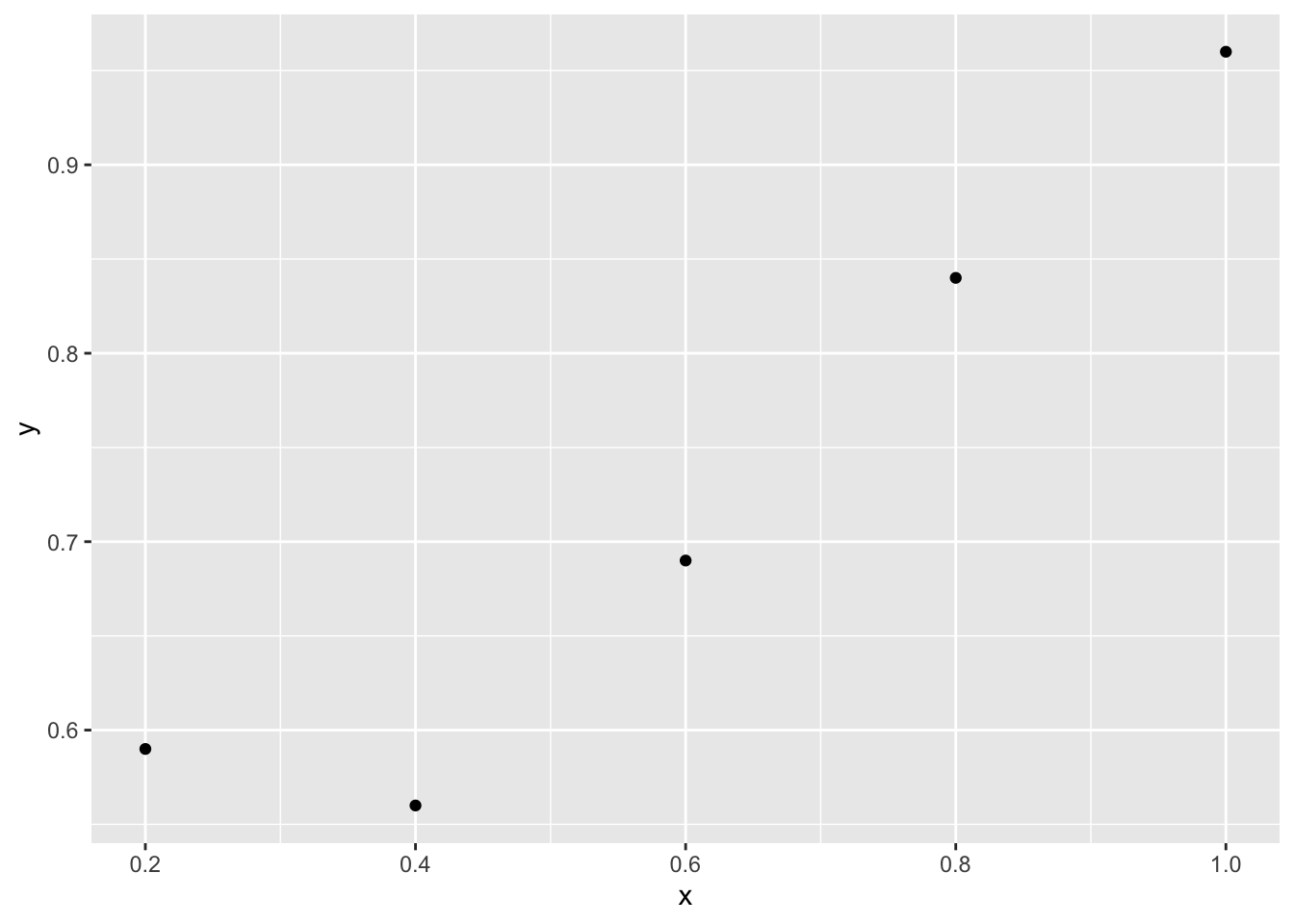 Given that the experiment is a 2-alternative forced choice, the lower asymptote should be 1/2. Let’s fit, for example, a MLE cumulative normal distribution
Given that the experiment is a 2-alternative forced choice, the lower asymptote should be 1/2. Let’s fit, for example, a MLE cumulative normal distribution
m <- 2
nll <- function(p) {
phi <- 1/m + (1 - 1/m) * pnorm(x, p[1], p[2])
-sum(k * log(phi) + (n - k) * log(1 - phi))
}
para <- optim(c(.7,.7), nll)$p
para## [1] 0.6681199 0.2533992xseq<-seq(0, 1, .01)
yseq <- 1/m + (1-1/m) * pnorm(xseq, para[1], para[2])
curve<-data.frame(xseq,yseq)
p<-p+geom_line(data=curve,aes(x=xseq,yseq))
p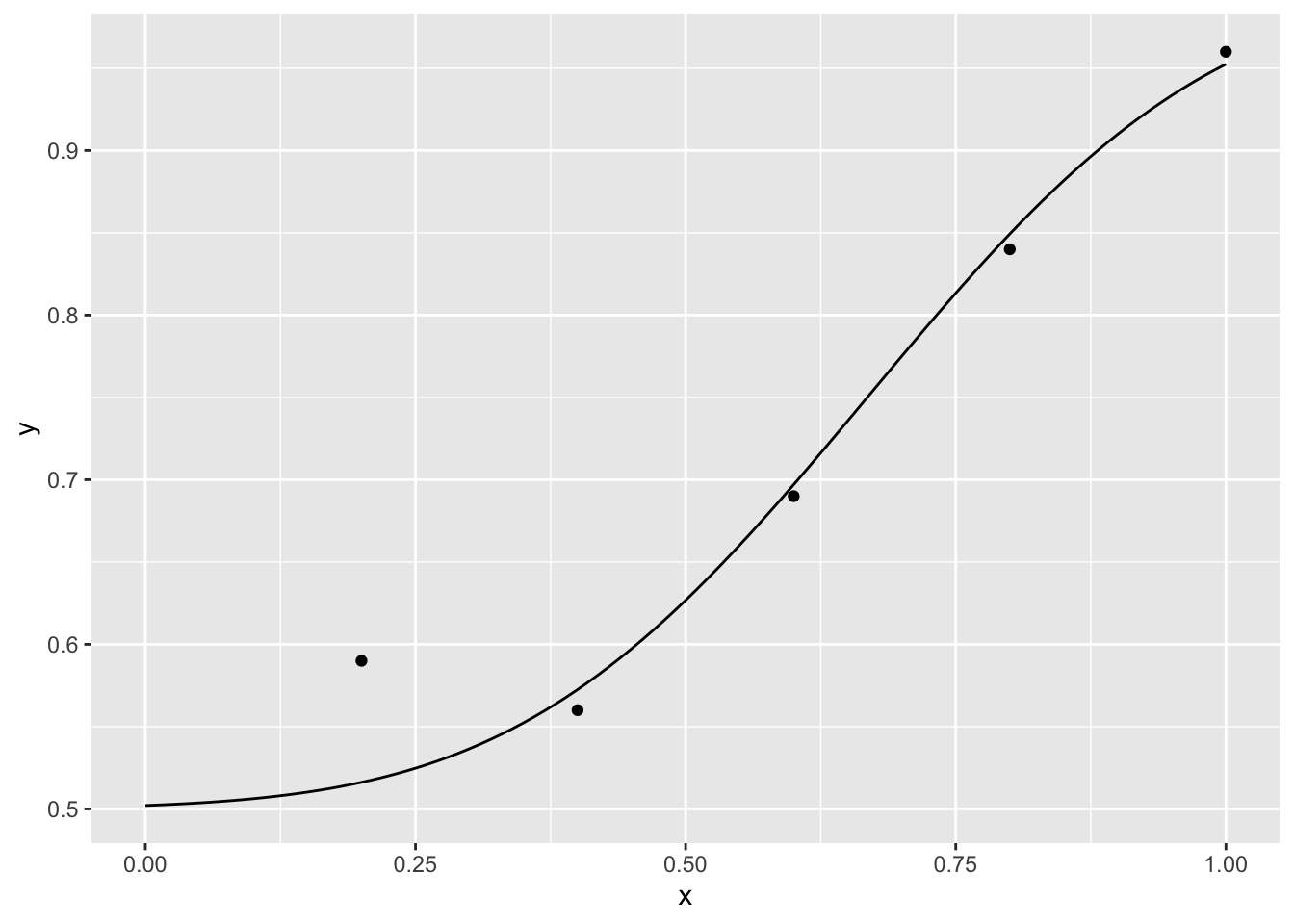
Threshold
We might be interested in calculating the luminance for which 80% of the responses are correct
ythre <- 0.8
thre <- qnorm((ythre - 1 / m) / (1 - 1 / m), para[1], para[2])
threshold <- data.frame(ythre,thre)
p + geom_linerange(data=threshold,aes(x=thre,ymin=.5,ymax=ythre))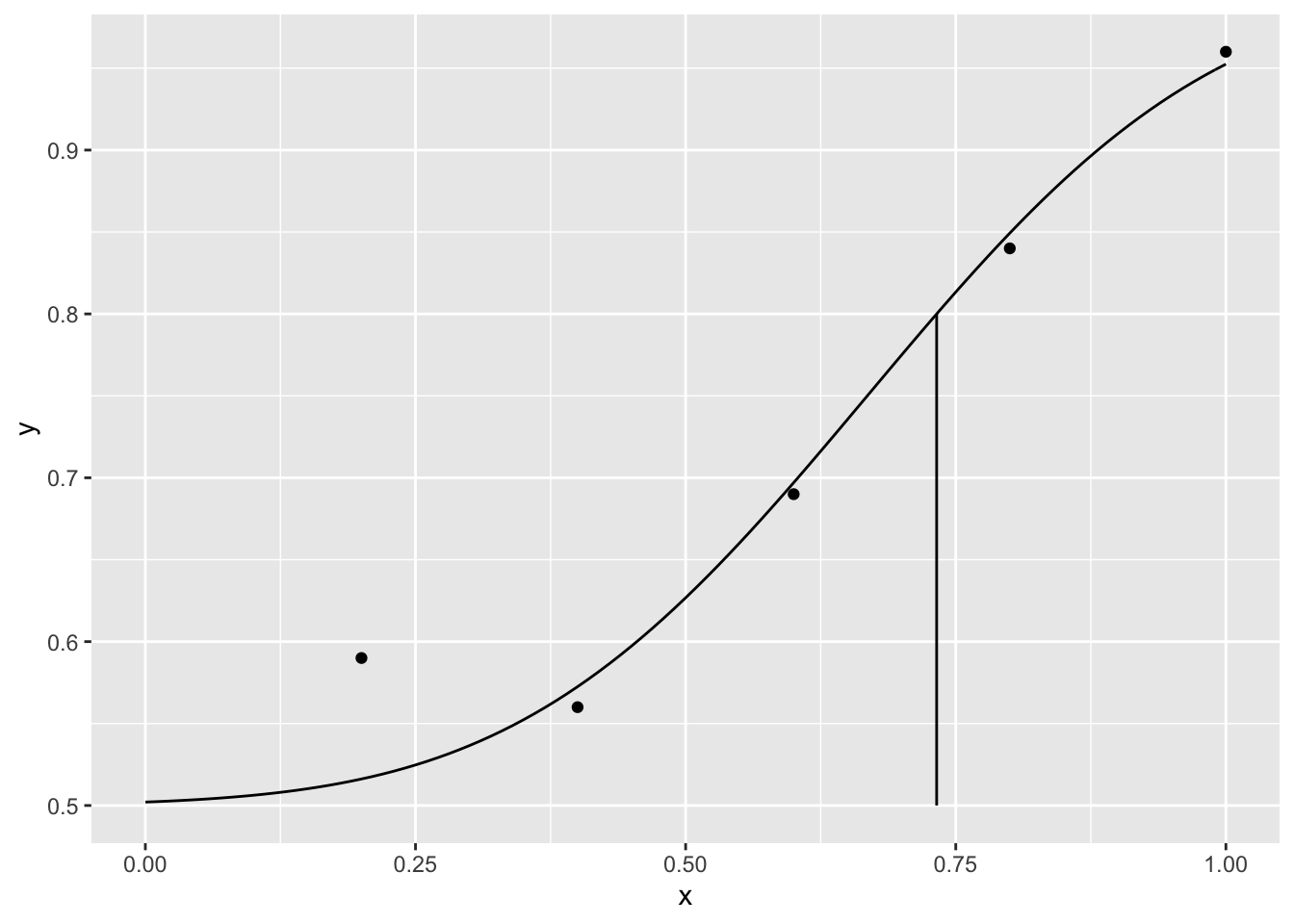
Fitting a gaussian curve
We can use a similar approach to fit a gaussian curve. A participant in one experiment, for example, needs to decide whether a flash and a sound are simultaneous or not for many possible asynchronies between the flash and the sound. For each asynchrony, the flash and sound are presented 100 times.
rm(list=ls())
n<-100
x<-seq(-.3,.3,.1) #asynchronies
k<-c(10,45,90,100,60,10,5) #simultaneous responses
r<-n-k
y<-k/100
dat<-data.frame(x,y,k,r)
gaussian<-function(x,p) exp(-0.5*((x-p[2])/p[3])^2)/(1+exp(-p[1]))
negLogL<-function(p,d,fun) {
phi<-fun(d$x,p)
-sum( d$k*log(phi)+d$r*log(1-phi) )
}
para<-optim(c(0,0.01,.2), negLogL,d=dat,fun=gaussian)$par
para## [1] 17.91232810 -0.03289997 0.12698617xSeq<-seq(-.3,.3,.01)
ySeq<-gaussian(xSeq,para)
ggplot()+
geom_point(data=dat,aes(x=x,y=y))+
geom_line(data=data.frame(xSeq,ySeq),aes(x=xSeq,y=ySeq))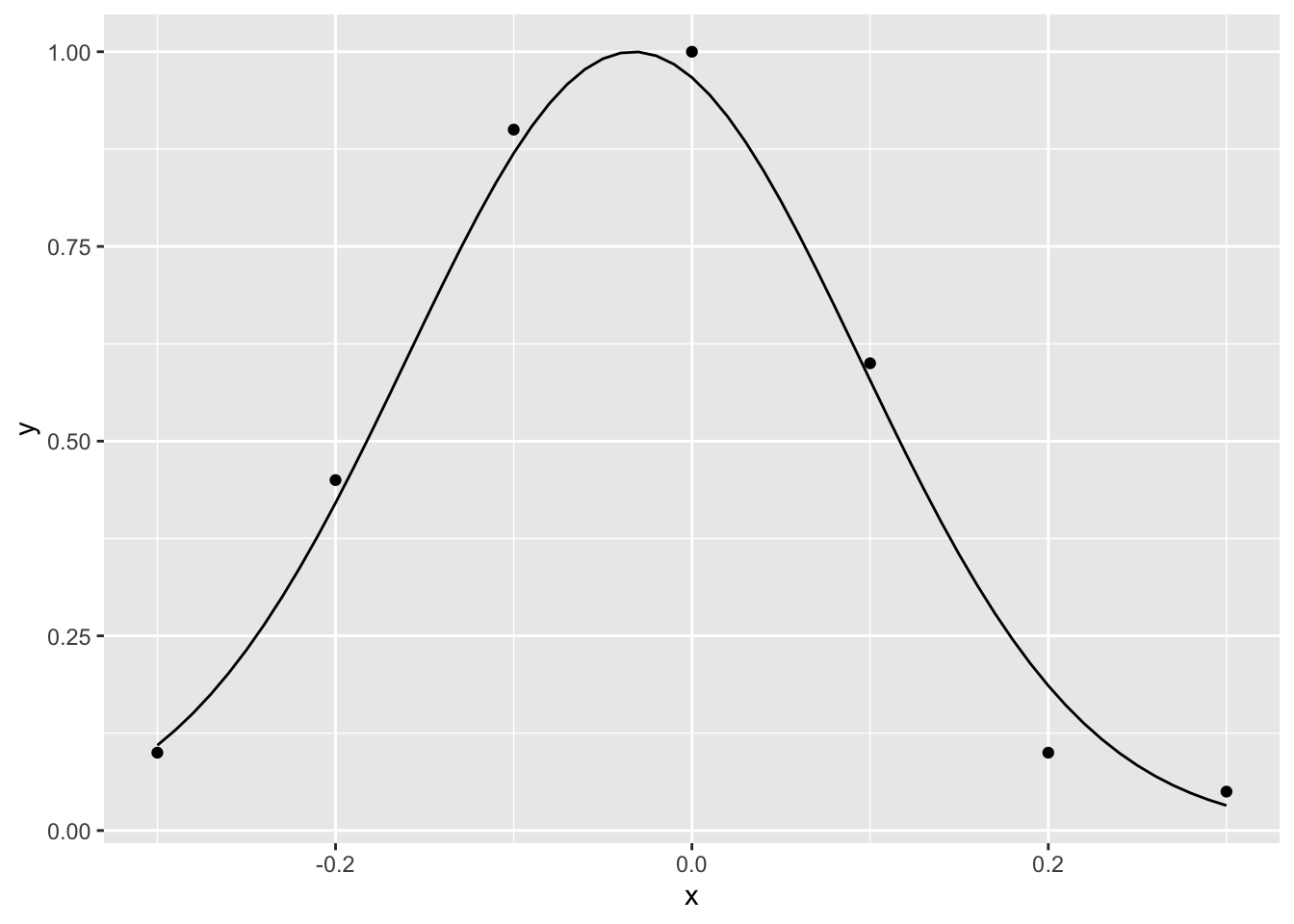
Fitting (using generalized linear models)
The psychometric function can be naturally considered within the framework of generalized linear models for which R has powerful tools (Knoblauch & Maloney (2012)). We can use this approach to fit the first example
n <- 100
x <- c(.2, .4, .6, .8, 1)
k <- c(10, 26, 73, 94, 97) # number of times that the observer reports that can see the stimulus
r <- n - k # number of times that the observer reports that cannot see the stimulus
y <- k/n
dat <- data.frame(x, y, k, r, n)
model <- glm( cbind(k, r) ~ x, data= dat, family = binomial(probit))
xseq <- seq(0, 1, .01)
yseq <- predict(model, data.frame(x = xseq), type = 'response')
curve <- data.frame(xseq, yseq)
p <- ggplot() +
geom_point(data = dat, aes(x = x, y = y)) +
geom_line(data = curve,aes(x = xseq, y = yseq))
p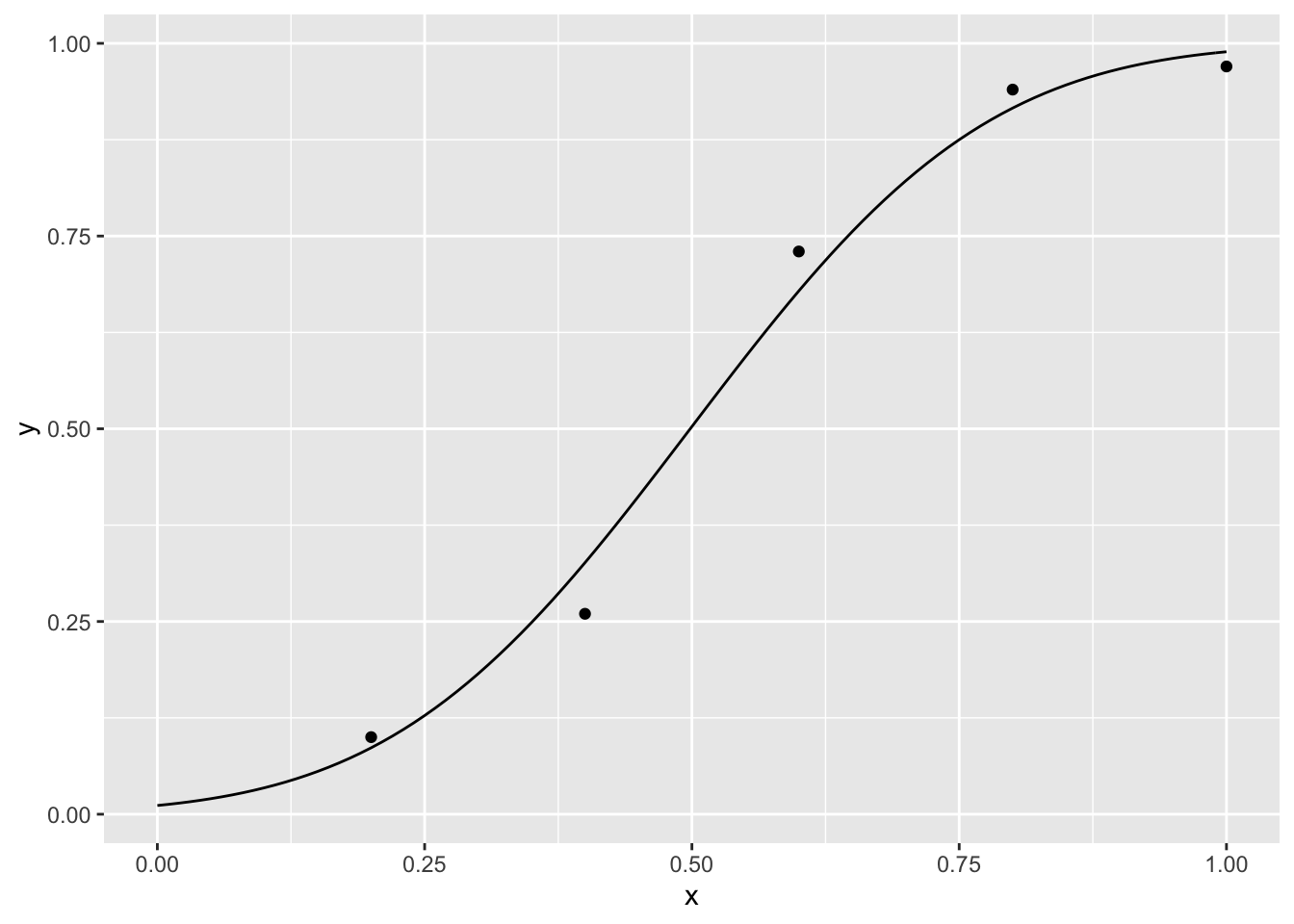 We use \(binomial\) because our response are distributed as a binomial variable and \(probit\) because we want to fit a cumulative normal curve. Given that the coefficients that returns \(glm\) are for the linear predictor we need to perform the following transformations to get the parameters.
We use \(binomial\) because our response are distributed as a binomial variable and \(probit\) because we want to fit a cumulative normal curve. Given that the coefficients that returns \(glm\) are for the linear predictor we need to perform the following transformations to get the parameters.
para <- c(-coef(model)[[1]] / coef(model)[[2]], 1 / coef(model)[[2]])
para## [1] 0.4984279 0.2187031If we want to fit data from m-alternatives forced choice, we can use the special link functions provided in the package \(psyphy\).
library(psyphy)
n <- 100
x <- c(.2, .4, .6, .8, 1)
k <- c(59, 56, 69, 84, 96)
r <- n - k
y <- k/n
dat <- data.frame(x, y, k, r, n)
m <- 2
model <- glm( cbind(k, r) ~ x, data= dat, family = binomial(mafc.probit(m)))
xseq <- seq(0, 1, .01)
yseq <- predict(model, data.frame(x = xseq), type = 'response')
curve <- data.frame(xseq, yseq)
p <- ggplot() +
geom_point(data = dat, aes(x = x, y = y)) +
geom_line(data = curve,aes(x = xseq, y = yseq))
p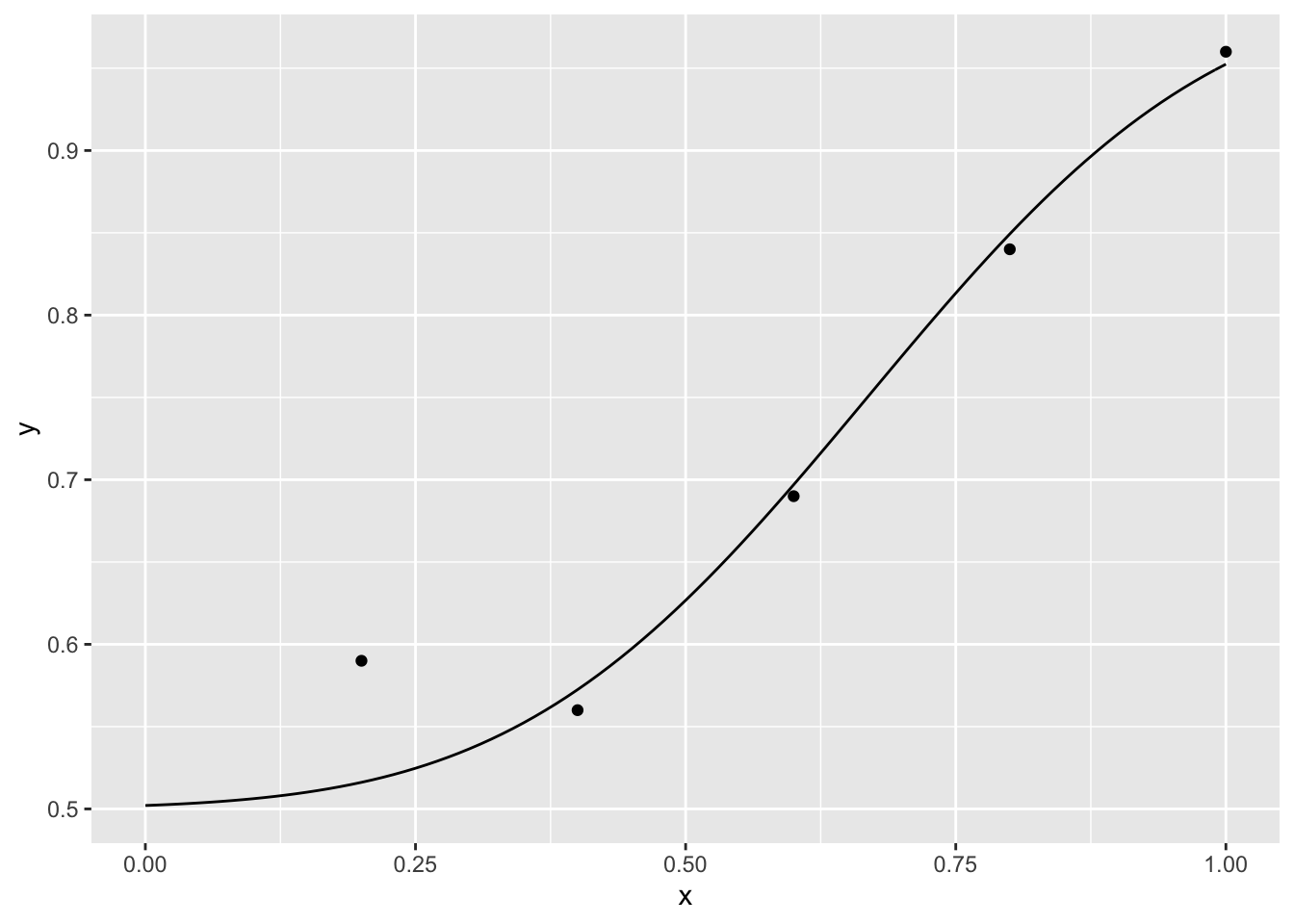
Parametric bootstrap confidence intervals
We start with the first example
n <- 100
x <- c(.2, .4, .6, .8, 1)
k <- c(10, 26, 73, 94, 97)
y <- k/n
dat <- data.frame(x, y, k, n)
nll <- function(p, d) {
phi <- pnorm(d$x, p[1], p[2])
-sum(d$k * log(phi) + (d$n - d$k) * log(1 - phi) )
}
para <- optim(c(.7, .7), nll, d = dat)$par # we need to pass the data to nll## Warning in pnorm(d$x, p[1], p[2]): NaNs producedxseq <- seq(0, 1, .01)
yseq <- pnorm(xseq, para[1], para[2])
curve <- data.frame(xseq, yseq)
p <- ggplot()+
geom_point(data = dat, aes(x = x, y = y)) +
geom_line(data = curve,aes(x = xseq, y = yseq))
p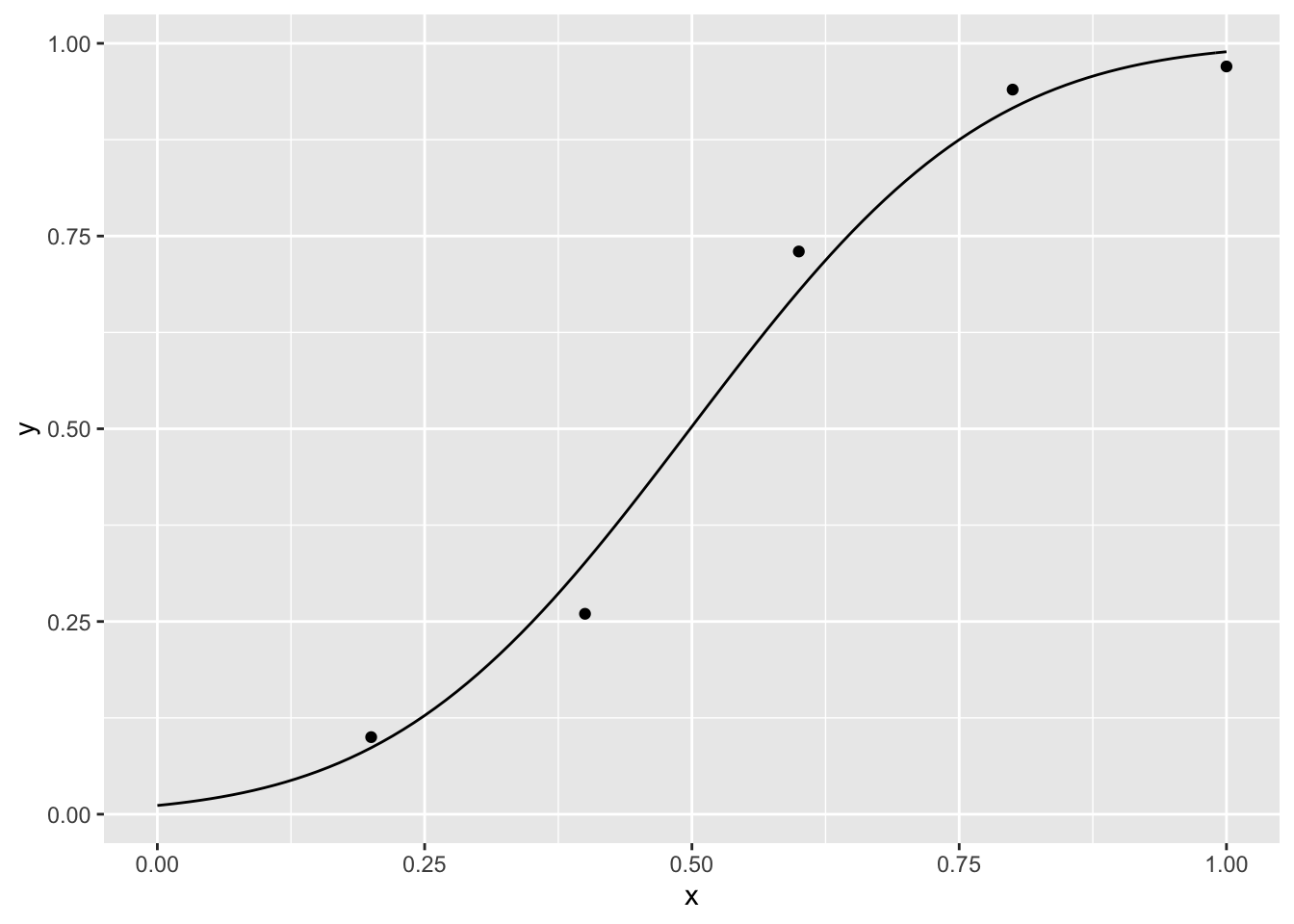
I create a 1000 samples of data frames that contain fake data simulated using a binomial distribution from the predicted data points of the fitted model. To avoid using explicit loops, I use the package \(dplyr\)
library(dplyr)ypred <- pnorm(dat$x, para[1], para[2])
sampling <- function(d){
k <- rbinom(length(dat$x), dat$n, ypred)
data.frame(x = dat$x, k, y = k/dat$n, n = dat$n)
}
fakedat <- data.frame(sample = 1:1000) %>%
group_by(sample) %>%
do(sampling(.))As an example I plot the 5 first samples
ggplot(data = filter(fakedat, sample < 6),
aes(x = x, y = y, color = factor(sample)))+
geom_line()+geom_point()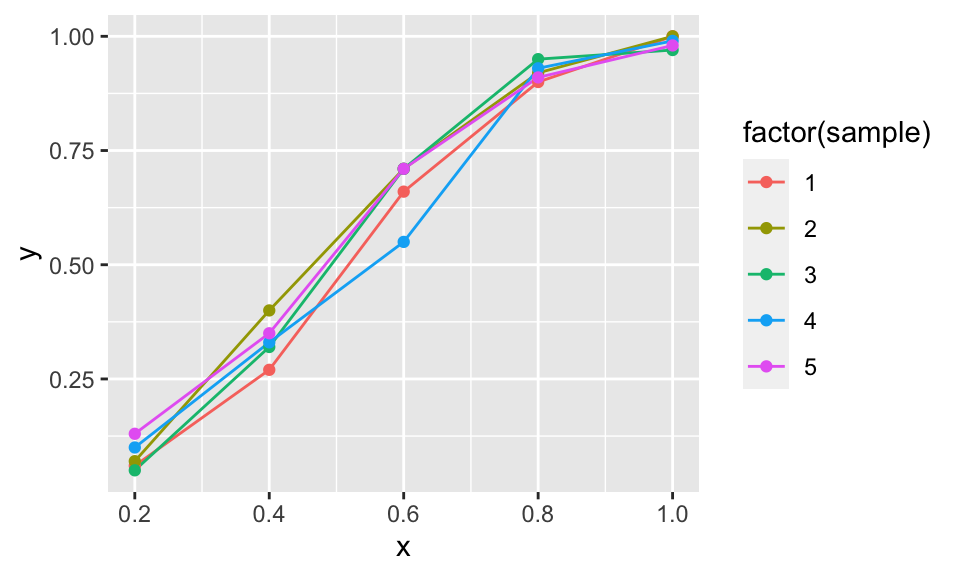
Then, I fit a model for each fake data sample and find the fake parameters of the cumulative normal curve (the mean and the standard deviation)
calculate_par<-function(d) {
para <-optim(c(.7,.7), nll, d = d)$par
data.frame(m = para[1], sta = para[2])
}
fakepar <- fakedat %>% group_by(sample) %>% do(calculate_par(.))and from the distribution of fake parameters, I calculate the confidence 95% intervals (using percentiles) for the parameters and plot the confidence intervals for the mean
ci_m <- quantile(fakepar$m, c(.025, .975))
ci_m## 2.5% 97.5%
## 0.4657812 0.5313473ci_sta <- quantile(fakepar$sta, c(.025, .975))
ci_sta## 2.5% 97.5%
## 0.1879236 0.2508350cid <- data.frame(min = ci_m[[1]], max = ci_m[[2]])
p + geom_segment(data = cid, aes(y = .5, yend = .5, x=min,xend=max))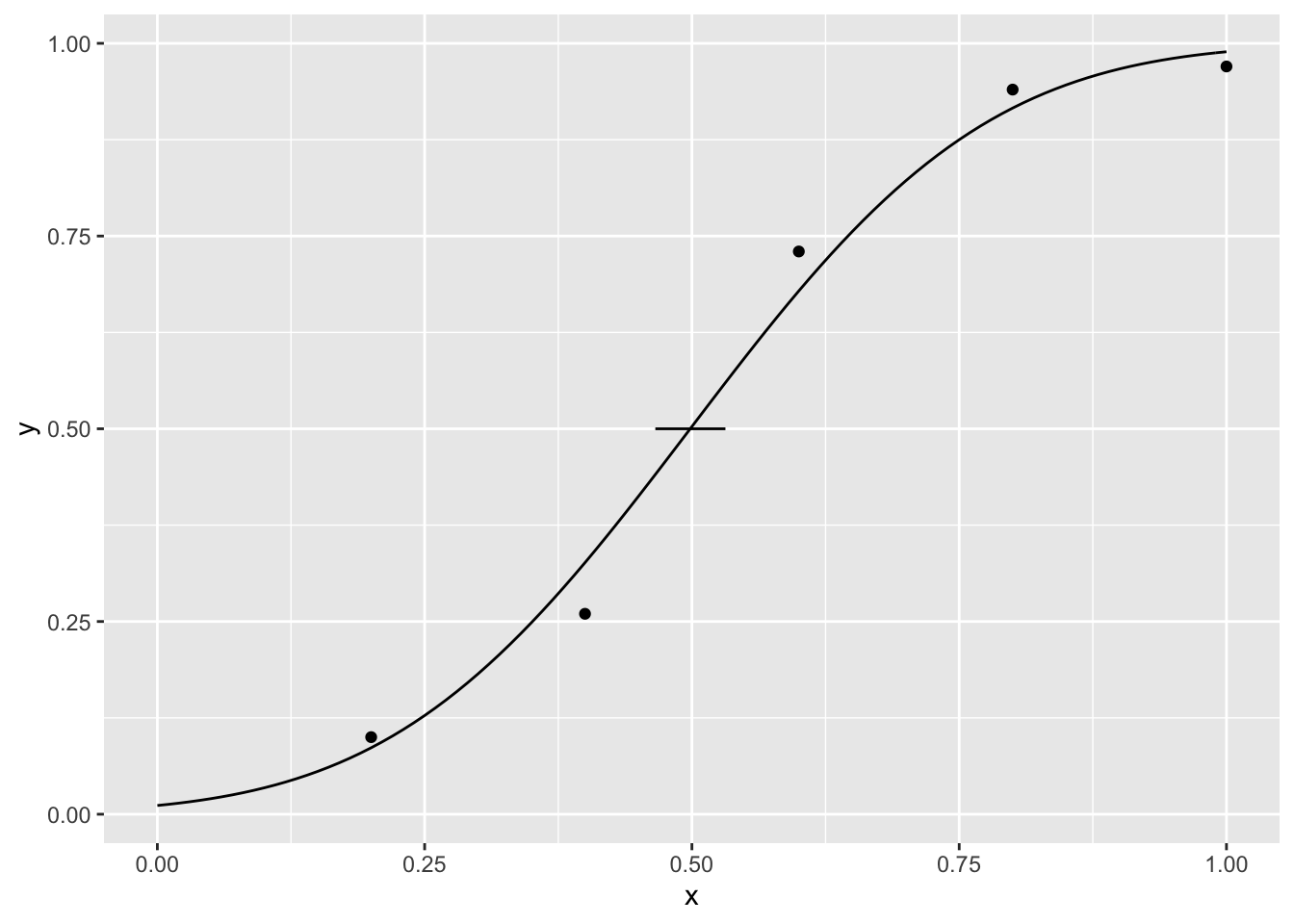
Parametric bootstrap confidence intervals using package \(boot\)
Instead of doing the bootstrap manually, we can use the function \(boot\) from the package with the same name.
library('boot')##
## Attaching package: 'boot'## The following object is masked from 'package:survival':
##
## aml## The following object is masked from 'package:lattice':
##
## melanomacalculate_sta <- function(d) optim(c(0.7, 0.7), nll, d = d)$par # as the bootstrap is parametric only requires the data as an argument
create_fake_data <- function(d , mle){ # it requires the data and another argument to help the computation that usually are the mle estimates but not in our case
k <- rbinom(length(d$x), d$n, mle)
data.frame(x = d$x, k, y = k/d$n, n = d$n)
}
myboot <- boot(dat, calculate_sta, R = 1000, sim = 'parametric',
ran.gen = create_fake_data, mle = ypred)
boot.ci(myboot, type = 'perc', index = 1) # c.i. for the mean## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myboot, type = "perc", index = 1)
##
## Intervals :
## Level Percentile
## 95% ( 0.4673, 0.5322 )
## Calculations and Intervals on Original Scaleboot.ci(myboot, type = 'perc', index = 2) # c.i. for the sta dev## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myboot, type = "perc", index = 2)
##
## Intervals :
## Level Percentile
## 95% ( 0.1883, 0.2511 )
## Calculations and Intervals on Original ScaleNon-parametric bootstrap confidence intervals
Now the fake data frames are create resampling the data, not the predicted data
sampling <- function(d){
k <- rbinom(length(dat$x), dat$n, dat$k / dat$ n) # here we use the data, not ypred
data.frame(x = dat$x, k, y = k/dat$n, n = dat$n)
}
fakedat <- data.frame(sample = 1:1000) %>%
group_by(sample) %>%
do(sampling(.))
calculate_par<-function(d) {
para <-optim(c(.7,.7), nll, d = d)$par
data.frame(m = para[1], sta = para[2])
}
fakepar <-fakedat %>% group_by(sample) %>%do(calculate_par(.))
ci_m <- quantile(fakepar$m, c(.025, .975))
ci_m## 2.5% 97.5%
## 0.4683718 0.5290537ci_sta <- quantile(fakepar$sta, c(.025, .975))
ci_sta## 2.5% 97.5%
## 0.1802335 0.2542283and using \(boot\)
myboot <- boot(dat, calculate_sta, R = 1000, sim='parametric',
ran.gen = create_fake_data, mle = dat$k / dat$n)
boot.ci(myboot, type = 'perc', index = 1) # c.i. for the mean## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myboot, type = "perc", index = 1)
##
## Intervals :
## Level Percentile
## 95% ( 0.4669, 0.5303 )
## Calculations and Intervals on Original Scaleboot.ci(myboot, type = 'perc', index = 2) # c.i. for the sta dev## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myboot, type = "perc", index = 2)
##
## Intervals :
## Level Percentile
## 95% ( 0.1810, 0.2538 )
## Calculations and Intervals on Original ScaleReferences
Knoblauch, K., & Maloney, L. T. (2012). Modeling Psychophysical Data in R. New York: Springer.
Prins, N., & Kingdom, F. A. A. (2010). Psychophysics: a practical introduction. London: Academic Press.
Wickham, H. (2014). Advanced R. Chapman; Hall/CRC.