library(tidyverse)

The binomial distribution is defined as

\[f(x; \theta) = f(k; n, p) = \binom{n}{k} p^k (1-p)^{n-k}\]

where \(n\) is often fixed. So we have \(f(k; p)\).


The problem in Probability theory

The parameter \(p\) is given and we can calculate the value of \(f\) for each posible value of \(k\).

Example 1:

Given \(p = 0.05\), the value of \(f\) for \(k=2\)?

\(f(k = 2; p = 0.05) = \binom{40}{2} 0.05^2 (1-0.05)^{38}\)

 dbinom(x = 2, size = 40, prob = 0.05)
## [1] 0.2776717

Example 2:

Given \(p = 0.05\), the value of \(f\) for \(k=13\)?

 dbinom(x = 13, size = 40, prob = 0.05)
## [1] 3.677303e-08

Example 3:

Given \(p = 0.25\), the value of \(f\) for \(k=13\)?

 dbinom(x = 13, size = 40, prob = 0.25)
## [1] 0.07590252


The problem in Statistics

The problem in statistics is the inverse. The value of \(k\) is given and we want to estimate \(p\).

The typical experiment to introduce the binomial distribution is about flipping coins, but let’s use a detection experiment instead


Point estimation

The value of \(k\) is given and we want to estimate \(p\)

The typical solution is to choose \(p\) for which \(f\) is maximum (maximun likelihood estiamtion, MLE). The MLE of \(p\) is typically written as \(\hat{p}\).

When considering \(f\) as a function of \(p\), \(f\) is called likelihood \(L(p)\)

Let’s plot it for \(k=3\)

lik_fun <- function(p) dbinom(x = 3, size = 40, prob = p)

tibble(p = seq(0, 1, .001)) |>  
  mutate(lik = lik_fun(p)) |>  
  ggplot(aes(p, lik)) +
  geom_line()

To find the maximum we calculate

\(\frac{dL}{dp} = 0\)

It could be demonstrated that the for binomial distribution \(\hat{p} = \frac{k}{n}\)

For example, for \(k=3\), \(\hat{p}\) ?

3/40
## [1] 0.075


Statistical model which is the product of two binomial distributions

\(f(k_1, k_2; p_1,p_2) = \binom{n}{k_1} {p_1}^{k_1} (1-p_1)^{n-k_1}\binom{n}{k_2} {p_2}^{k_2} (1-p_2)^{n-k_2}\)

Example:

In 40 trials where the probability was \(p_1\), \(k_1 =3\)

In 40 trials where the probability was \(p_2\), \(k_2 =16\)

\(L(3, 16;p_1, p_2)\)

The MLE of \(p_1\)

3/40
## [1] 0.075

The MLE of \(p_2\)

16/40
## [1] 0.4


Statistical model which is the product of five binomial distributions

\[f(k_1, \cdots,k_5; p_1,\cdots,p_5) = \prod_{i=1}^{5} \binom{n}{k_i} {p_i}^{k_i} (1-p_i)^{n-k_i}\]

Example

dat <- tibble(k = c(2, 16, 26, 32, 38), n = 40)
dat
## # A tibble: 5 × 2
##       k     n
##   <dbl> <dbl>
## 1     2    40
## 2    16    40
## 3    26    40
## 4    32    40
## 5    38    40

\(L(2, 16, 26, 32, 38; p_1, p_2, p_3, p_4,p_5)\)

dat <- dat |> 
  mutate(p_mle = k /n)

dat
## # A tibble: 5 × 3
##       k     n p_mle
##   <dbl> <dbl> <dbl>
## 1     2    40  0.05
## 2    16    40  0.4 
## 3    26    40  0.65
## 4    32    40  0.8 
## 5    38    40  0.95

We have a model with

A model in which we have a parameter for every observation is called the saturated model.

It is the maximum overfitting that we can do.

Because the likelihood involves many multiplications and it is very small, usually we use the logarithm of the likelihood. As the log likelihood is a monotonic transformation of the likelihood, the maximum of the log likelihood is the same as the maximum of the likelihood.

\[L(p_1,\cdots,p_5) = \sum_{i=1}^{5} \left( log \binom{n}{k_i} + {k_i}log({p_i})+({n-k_i}) log (1-p_i) \right)\]

The log likelihood of the saturated model is (the binomical coefficient is typically dropped as it does not depend on the parameters and does not affect the maximum likelihood estimation)

log_lik_saturated_fun <- function(p) {
  
  # p <- pmax(pmin(p, 0.9999), 0.0001) # Very important if optimization is performed to avoid log(0) and log(1) !!
  sum(lchoose(dat$n, dat$k) + dat$k * log(p) + (dat$n - dat$k) * log(1 - p))
}

and the maximum likelihood of the saturated model is

log_lik_saturated_fun(dat$p_mle)
## [1] -8.507216

The models with less parameters will have a log likelihood smaller than this.


Psychometric funcion

We reduce the number of parameters by expressing \(p_i\) in terms of an indexing variable \(x_i\) and less parameters

\[p_i = \gamma +(1- \gamma - \lambda) F(x_i;\mu, \sigma)\]

Where \(F\) is a function with a sigmoidal shape and \(\gamma\) and \(\lambda\) are parameters that are used to adjust the range of the function.

This expression for \(p_i\) is called the psychometric function (it has 4 parameters)

Let’s fix \(\gamma=0\) and \(\lambda = 0\) (2 parameters)

\[p_i = \Phi(x_i;\mu, \sigma)\]

An example of \(F\) is the logistic function

tibble(x = seq(-5, 5, .01)) |> 
  mutate(phi = 1 / (1 + exp(-1 - 2 * x))) |> 
  ggplot(aes(x, phi)) +
  geom_line()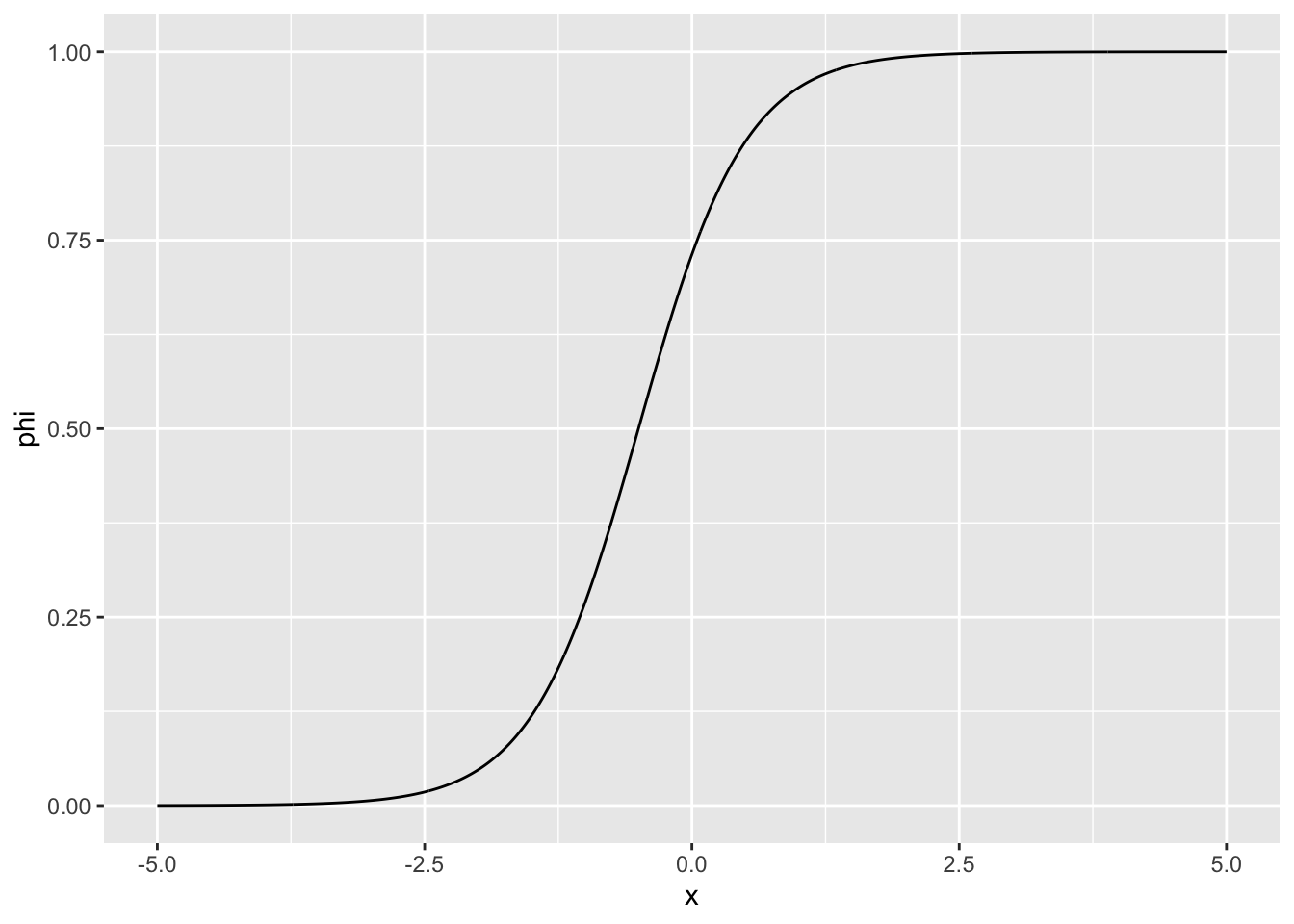

So the model we are fitting to the detection experiment is

\[f(k_1, \cdots,k_5; \mu, \sigma) = \prod_{i=1}^{5} \binom{n}{k_i} {\Phi(x_i;\mu, \sigma)}^{k_i} (1-\Phi(x_i;\mu, \sigma))^{n-k_i}\]

Let’s consider that our indexing variable is contrast

dat <- tibble(contrast = c(0, 1, 2, 3, 4), k = c(2, 16, 26, 32, 38), n = 40)
  
dat
## # A tibble: 5 × 3
##   contrast     k     n
##      <dbl> <dbl> <dbl>
## 1        0     2    40
## 2        1    16    40
## 3        2    26    40
## 4        3    32    40
## 5        4    38    40

So we are hypothesizing that \(p_i\) increases with contrast.

We can plot \(k\) as a function of contrast

dat |> 
  ggplot(aes(contrast, k)) +
  geom_point() +
  ylim(0,40)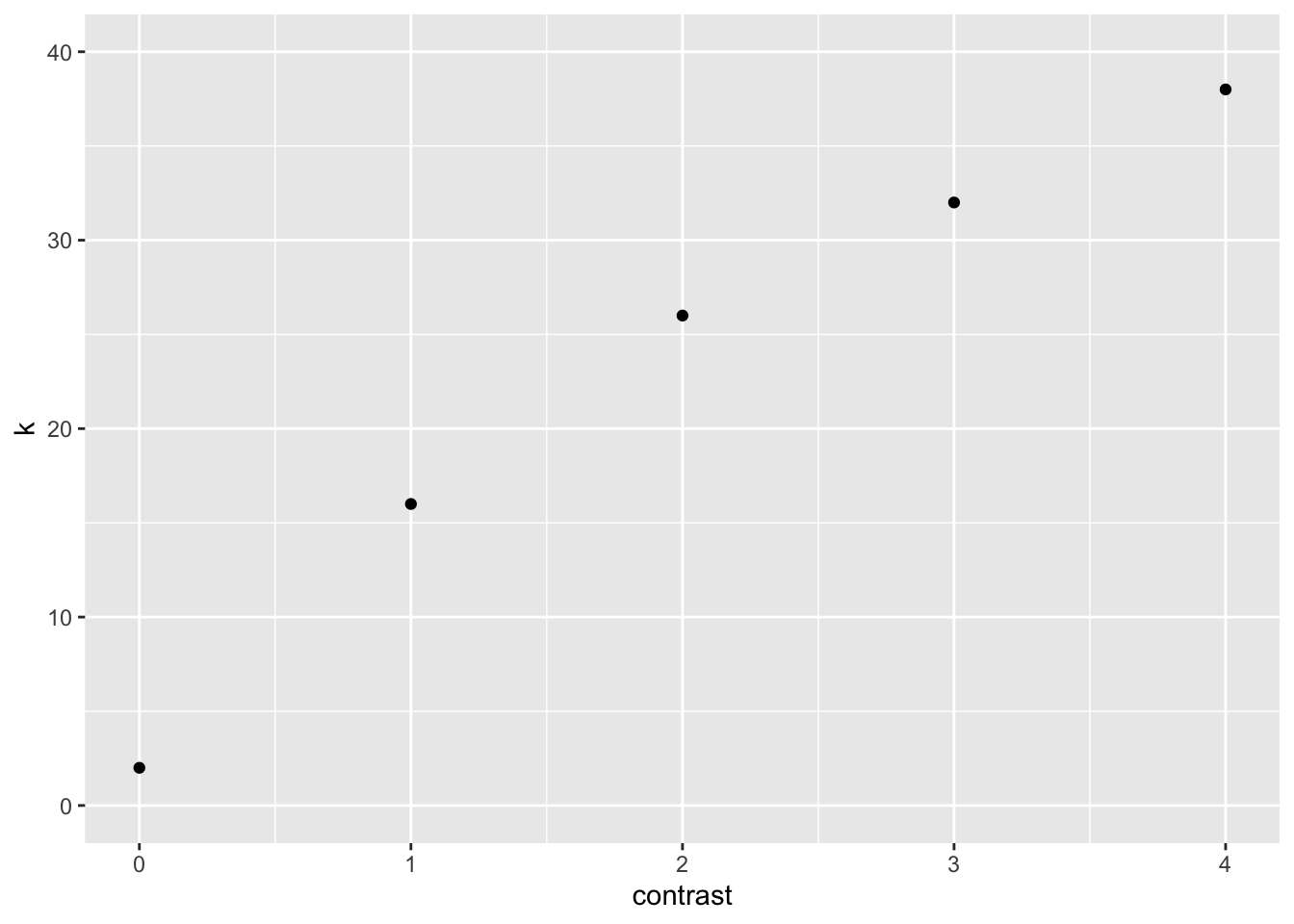

or the probability of detecting (which indeed correspond to the best estimation of the parameters of the saturated model) as a function of contrast

dat <- dat|> 
  mutate(p = k /n )

dat |> 
  ggplot(aes(contrast, p)) +
  geom_point() +
  ylim(0,1)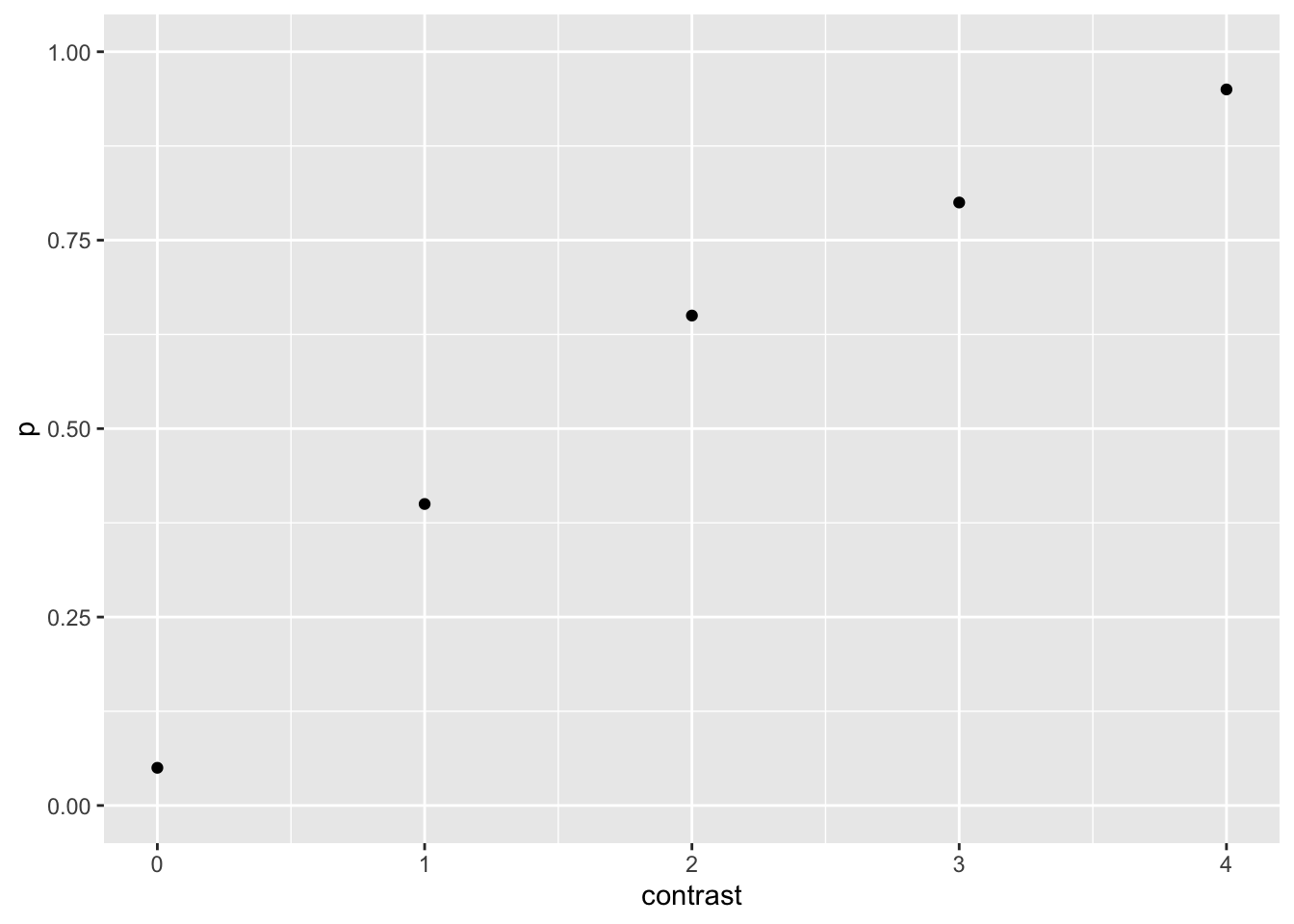

The log likelihood of tha saturated model was

log_lik_saturated_fun <- function(p) { # p is a vector of 5 parameters
  sum(lchoose(dat$n, dat$k) + dat$k * log(p) + (dat$n - dat$k) * log(1 - p))
}

and the log likelihood of the psychometric function model is

log_lik_fun <- function(p) { #p is a vector of 2 parameters: mu and sigma
  phi <-  1 / (1 + exp(-p[1] - p[2] * dat$contrast))
  sum(lchoose(dat$n, dat$k) + dat$k * log(phi) + (dat$n - dat$k) * log(1 - phi))
}

Let´s look at some log lik

log_lik_fun(c(3, 1))
## [1] -264.8652
log_lik_fun(c(1.5, 1))
## [1] -145.7988

Let’s find the values of \(p_1\) and \(p_2\) that maximize the log lik

neg_log_lik_fun <- function(p) -log_lik_fun(p) 

mle_par <- optim(c(1, 1), neg_log_lik_fun)$par 

mle_par
## [1] -2.018336  1.246996

So the psychometric function is

psy_curve <- tibble(contrast = seq(0, 4, .1)) |>  
  mutate(p =  1 / (1 + exp(-mle_par[1] - mle_par[2] * contrast)))

Let’s added to the previous plot

  ggplot() +
  geom_point(data = dat, aes(contrast, p)) +
  geom_line(data = psy_curve, aes(x = contrast, y = p)) +
  ylim(0,1)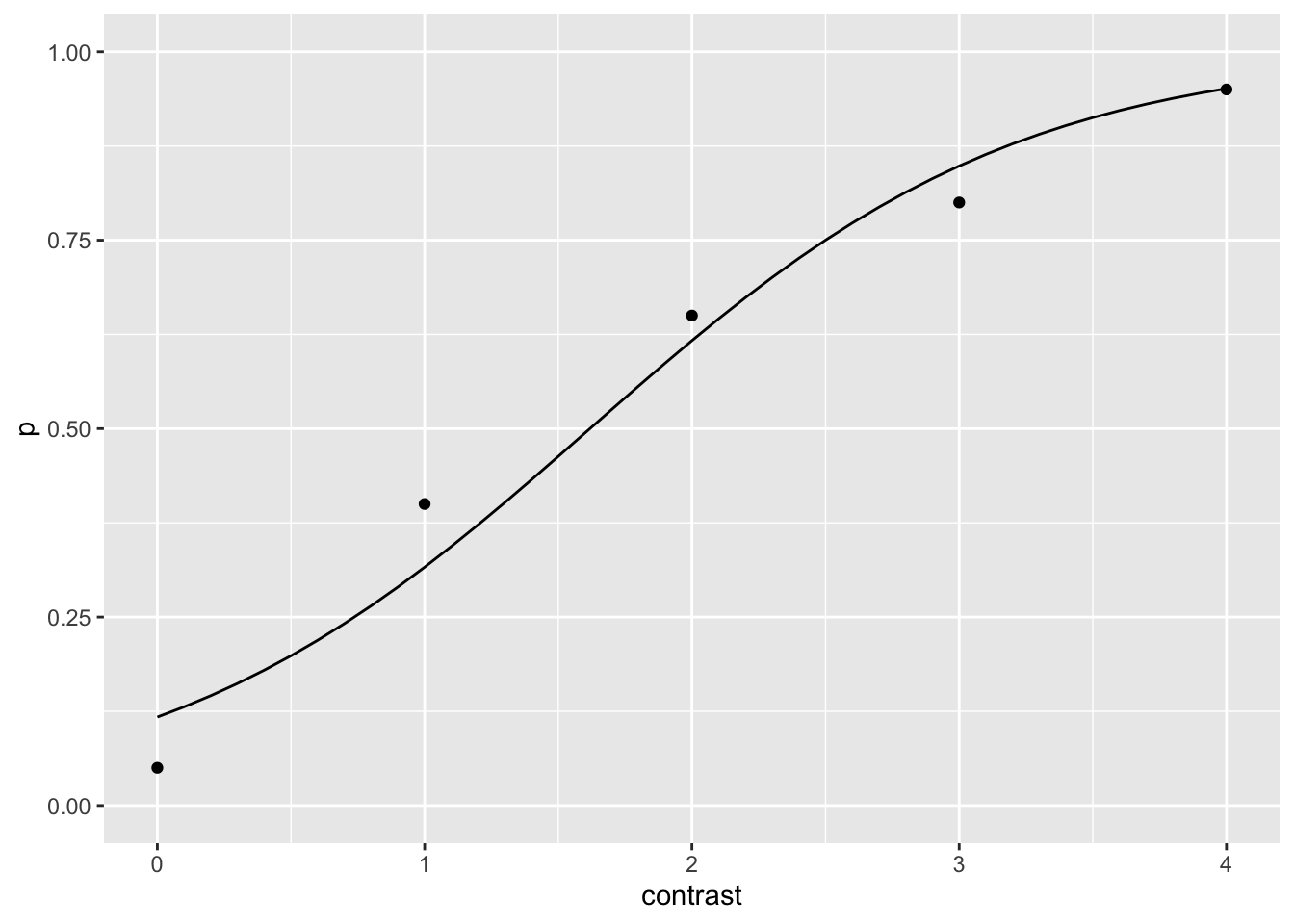

The likelihood of the model for the MLE parameters

log_lik_fun(mle_par)
## [1] -10.65097